在数学中,特别是线性代数中,我们常常会遇到齐次方程和非齐次方程。\begin{cases}2x+3y=0\\4x-2y=0\end{cases})这是一个齐次方程组,因为方程的右侧都是零。D)不为零,那么这个方程组就是非齐次的。理解齐次和非齐次方程的概念可以通过对方程中的常数项进行观察。齐次方程相比非齐次方程更简单,因为它们总是有零解,而非齐次方程可能有唯一解、无解或无穷多解。

在数学中,特别是线性代数中,我们常常会遇到齐次方程和非齐次方程。
1. 齐次方程:
- 如果一个线性方程组的常数项都为零,那么它就是一个齐次方程组。
- 例如,对于方程组:
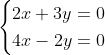
这是一个齐次方程组,因为方程的右侧都是零。
- 更一般地,对于线性方程组 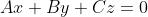 ,如果  都为零,那么这个方程组就是齐次的。
2. 非齐次方程:
- 如果一个线性方程组的常数项中至少有一个不为零,那么它就是一个非齐次方程组。
- 例如,对于方程组:
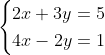
这是一个非齐次方程组,因为方程的右侧都不是零。
- 更一般地,对于线性方程组 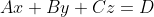 ,如果 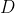 不为零,那么这个方程组就是非齐次的。
理解齐次和非齐次方程的概念可以通过对方程中的常数项进行观察。如果没有常数项或常数项为零,那么方程就是一个齐次方程;如果常数项不为零,那么方程就是一个非齐次方程。齐次方程相比非齐次方程更简单,因为它们总是有零解,而非齐次方程可能有唯一解、无解或无穷多解。
